DeepSeekMath-V2 (paper, model) is a self-verifiable mathematical reasoning model developed by DeepSeek-AI. It can both solve problems and verify its own reasoning, making it especially powerful for proof-based tasks such as IMO-style problems and theorem proving.
DeepSeekMath-V2 is designed for:
- Solving competition-level math problems
- Producing complete, logically consistent proofs
- Acting as a “self-debugging” mathematical assistant
- Checking its own reasoning and iteratively refining the proof until errors are resolved
- Exploring new conjectures or theorem-like tasks
DeepSeekMath-V2 marks a shift from traditional answer-focused approaches toward truly reasoning-centered AI. But why does this matter? An AI must reason correctly in mathematics in order to be trusted to make accurate decisions in domains such as physics, finance, engineering, or any context where even small mistakes can have significant consequences.
Installation and setup
DeepSeekMath-V2 builds directly on the DeepSeek-V3.2-Exp architecture, which provides all the conversion scripts, serving tools, and runtime settings. Math-V2 only provides the optimized weights trained specifically for mathematical reasoning. You must primarily follow the instructions provided by the DeepSeek-V3.2-Exp repository.
- Conversion: You must first use the V3.2-Exp tools to convert the DeepSeekMath-V2 weights into the proprietary, optimized format required by the DeepSeek serving engine, specifying the path using the
--hf-ckpt-pathflag. - Inference: You then run the V3.2-Exp inference engine, loading the newly converted Math-V2 weights instead of the general-purpose weights.
⚠️ The DeepSeek-V3.2-Exp architecture is a massive 685-billion parameter Mixture-of-Experts (MoE) model that requires data center-grade hardware (multiple A100 or H100 GPUs).
For better results you should write clear, structured prompts, such as: “Provide a detailed, step-by-step proof”, “Check the correctness of this solution” or “Identify gaps or errors in the argument.” For example:
Problem: Prove that if a, b, c > 0 and abc = 1, then a2+b2+c2 ≥ ab + bc + ca.
Task: Your task is to provide a detailed, step-by-step proof suitable for an Olympiad solution and verify the correctness of each step.
The problem of theorem proving with LLMs
Over the past few years, LLMs like GPT and Claude have become better at solving math problems. Using reinforcement learning, many models learned to solve competition-level problems, such as AIME and HMMT, that primarily evaluate final answers.
They also acquired the ability to solve certain IMO-style tasks, which are based on step-by-step reasoning. However, the reward mechanism used in reinforcement learning proves inefficient for theorem-proving tasks, being constrained by two major limitations:
- Lack of process validation: The reward signal evaluates only the final answer and does not assess whether the reasoning steps are logically correct.
- Incompatibility with theorem proving: In theorem proving, the validity of each reasoning step is more important than the conclusion itself. Rewarding only the final answer provides no guidance for verifying or improving the step-by-step reasoning process.
The AI systems should be capable of genuine reasoning rather than simple output generation. A promising direction is the integration of self-verification, in which the model evaluates its own solutions to ensure the correctness of its reasoning. This capability is especially valuable for tasks where the answer is not known in advance, such as the discovery of new theorems.
However, self-verification systems have no clear separation (gap) between generating and verifying. The same large model that generates a proof is often doing the verification at the same time. Without separating these roles, advancing the capabilities of natural-language theorem provers becomes significantly more difficult.
The model
DeepSeekMath-V2 is built on DeepSeek-V3.2-Exp-Base, developed by researchers at DeepSeek-AI. The model explicitly separates proof generation from verification through two core components:
- Proof generator: A large language model responsible for producing candidate proofs.
- Neural verifier + meta-verifier: LLMs trained to evaluate step-by-step proofs.
The proof generator uses that verifier as a reward signal and is encouraged to self-review and refine until the verifier (and meta-verifier) accept the proof.
Evaluation
The evaluation tested the model’s performance in mathematical reasoning across multiple settings.
One-shot generation: DeepSeekMath-V2 was first tested on its ability to produce correct proofs without refinement. For each problem, 8 proofs were generated and verified. Across all categories (algebra, geometry, number theory, combinatorics, and inequalities) the model consistently outperformed leading models such as GPT-5-Thinking-High and Gemini 2.5-Pro, showing better theorem-proving ability across domains (see the next figure).

Sequential refinement with self-verification: For competition-level problems such as those from the IMO and CMO, a single attempt often fails due to token limits. DeepSeekMath-V2 uses a multi-step refinement process, where it generates a proof, self-verifies it, then uses its own output and verification feedback to iteratively improve the proof. Two metrics were used: Pass@1 (average proof quality) and Best@32 (best proof selected by the model itself).

The picture above shows that on IMO Shortlist 2024 problems both metrics improved as the number of refinement iterations increased, confirming the model’s ability to identify flawed proofs and improve them successfully through self-verification. The proof score ranges from 0.0 (incorrect or logically inconsistent) to 1.0 (fully correct).
- Pass@1 (blue): The model generates only a single proof attempt. Its score increases from 0.15 at one iteration to 0.27 after eight iterations.
- Best@32 (orange): The model produces up to 32 candidate proofs, and the best valid one is selected. This score begins at 0.26 and reaches 0.42 with eight iterations.
High-compute search: For the most difficult problems, DeepSeekMath-V2 combined large-scale generation with extensive verification. It maintained a large pool of candidate proofs, used extensive verification to pinpoint issues, and generated many parallel refinements. As can be seen in the table below, this compute-intensive search process proved highly effective:
- IMO 2025: solved 5 of 6 problems (83.3%)
- CMO 2024: solved 4 problems fully, with partial credit on another (73.8%)
- Putnam 2024: solved 11 of 12 problems, scoring 118/120—well above the top human score of 90

On the IMO-ProofBench benchmark (see the next picture), the model outperformed or was competitive with the strongest existing models, such as Gemini Deep Think.
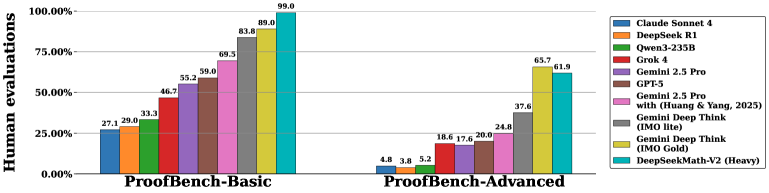
All scores were drawn from Luong et al. (2025) except those for DeepSeekMath-V2, which were assessed by the authors’ own experts.
Conclusion
DeepSeekMath-V2 adds self-verification to transform math LLMs from “answer machines” and simple problem-solving tools into full reasoning systems capable of generating, evaluating, and refining mathematical arguments.
This is especially important in research contexts where correctness cannot be benchmarked against known solutions. By embedding self-verification, models like DeepSeekMath-V2 demonstrate that AI can move closer to genuine mathematical reasoning rather than superficial output generation.






